נ ק ו ד ה
- ההגדרה של נקודה היא שזהו מקום חסר ממדים במרחב .
- רצף של נקודות מהווה קו .
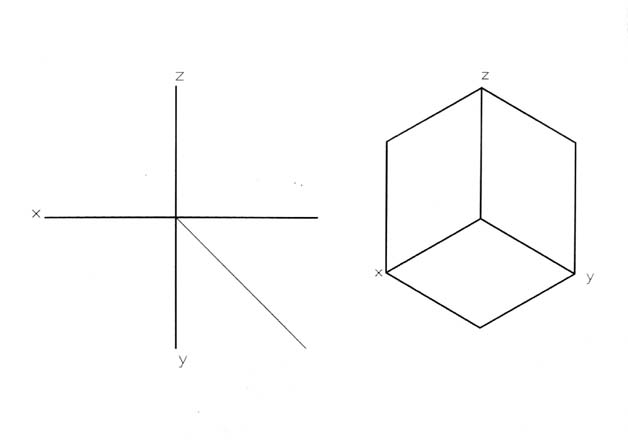
- לקווים הנוצרים במפגש של שלושת הלוחות קוראים - צ י ר י ם : והם מסומנים באותיות x , y , z .
- כל נקודה במרחב ניתנת לתיאור על גבי מישורי הטלה באמצעות קרניים העוברות דרכה - הניצבות והפוגעות במישור ההטלה .
- מרחקה של נקודה במרחב מסומן באמצעות 3 אותיות ( המסמלות מספרים ) בתוך סוגריים :
- הנקודה מסומנת בדרך כלל באות לועזית - P ומיקומה במרחב יסומן בצורה הבאה : ( P ( a , b , c .
a = מרחקה של הנקודה לאורך ציר ה - x .
b = מרחקה של הנקודה לאורך ציר ה - y .
c = מרחקה של הנקודה לאורך ציר ה - z .
- הנקודה הנמצאת במפגש שלושת הלוחות מסומנת ב ( 0 , 0 , 0 ) , כי הנקודה נמצאת במרחק 0 מכל שלושת הלוחות .
המישור שעליו מוטל מבט הפנים נקרא : π2
המישור שעליו מוטל מבט הצד נקרא : π3
- על כל מישור מופיעים שני שיעורים של הנקודה :
- על π1 מופיעים המרחקים בכיוון ציר ה x ובכיוון ציר ה y .
- על π2 מופיעים המרחקים בכיוון ציר ה x ובכיוון ציר ה z .
- על π3 מופיעים המרחקים בכיוון ציר ה y ובכיוון ציר ה z
הקשר בין נקודה קו ומישור .
- חשיבות מציאת מיקומה של נקודה בתוך הלוחות השונים :
- מציאת נקודות היא הבסיס לכל שפת השרטוט ומכאן חשיבותן .
- אם אנו יודעים למצוא נקודה אחת - אנו יכולים למצוא באותה דרך בדיוק עוד ועוד נקודות , ואם נחבר שתי נקודות הרי שהצלחנו למצוא קו , ואם נמשיך ונמצא עוד קוים באמצעות הנקודות - אנחנו מסוגלים למצוא משטחים ואם נצרף זה לזה כמה משטחים - נמצא שאנו מסוגלים לתאר צורות בעלות נפח תלת ממדי - וכל זה , על הנייר .
כל זוג של מישורי הטלה נקרא מ י ש ו ר י ם צ מ ו ד י ם .
- כל שני היטלים של אותה הנקודה על מישורים צמודים - קשורים ביניהם באמצעות קו עזר הנקרא ק ו צ מ ד .
ק ו צ מ ד הוא קו ישר המאונך לציר שבין שני מישורי הטלה צמודים .
- על קו הצמד נמדדים המרחקים של הנקודה ממישורים אלה .
- כאשר המישורים הצמודים הם - π1 ו π2 המרחק מ π2 מופיע על π1 ועל
π2 מופיע המרחק מ π1 .
- כאשר a , b , c נתונים ביחידות מידה ( במספרים ), קובעים את מערכת הצירים במקום רצוי על פני הגליון ואז מודדים את שיעורי הנקודה בכיווני הצירים המתאימים .
- כאשר יש לנו גם היטל שלישי - π3 אז גובהה של הנקודה מתקבל על ידי קו צמד מההיטל השני ואילו מרחקה מציר z הוא שיעור ה y של הנקודה .
שמות של נקודות :
- נ ק ו ד ה מ י ש ו ר י ת : נקודה שאחד משלושת מרחקיה מהקואורדינטות שווה לאפס נקראת נקודה מישורית .
- נ ק ו ד ה צ י ר י ת : נקודה ששניים משלושת מרחקיה מהקואורדינטות שווים לאפס נקראת נקודה צירית .
- נ ק ו ד ה מ ר כ ז י ת : נקודה אשר כל מרחקיה מהקואורדינטות שווים לאפס נקראת נקודה מרכזית .
- נ ק ו ד ה מ ר ח ב י ת : נקודה אשר כל מרחקיה ממערכת הצירים שונים מאפס נקראת נקודה מרחבית .
נקודות נסתרות :
- ק ו מורכב מרצף אינסופי של נקודות .
- ק ט ע הוא חלק של קו המוגבל על ידי שתי נקודות - נקודה אחת בתחילתו ונקודה שניה בסופו של הקטע .
- כאשר אנו עומדים במצב שבו אנו רואים את נקודת ההתחלה של קטע ישר והקטע עצמו מתרחק מאיתנו בניצב לקו האופק שלנו - כל הקטע ייראה לנו כנקודה אחת בלבד , כי נקודת הסוף של הקטע מוסתרת על ידי הנקודה הראשונה . נקודה המוסתרת על ידי נקודה שנמצאת לפניה נקראת נ ק ו ד ה נ ס ת ר ת , כי היא קיימת אך אנו לא רואים אותה .
ה י ט ל י ם נ ו ס פ י ם של נקודה :
- קיימים מצבים בהם עלינו להוסיף מישורי הטלה נוספים בנוסף לשלושת המישורים π2 , π1 , ו π3 , ואז נראה את הנקודה בהיטליה הנוספים על המישורים שהוספנו .